logo
Log in
  Get Rs 200 off on Oswal Premium Plan for your board preperatoin! For Class 9th till 12th. Use Coupon Code BOARD200 at checkout.
logo
Log in
Start Free Trial
Mensuration

Home / Board / ICSE / important Questions / Class 10 / Maths / Mensuration

Class 10 Maths Chapter 17
Mensuration
Important Questions

exam preparation with oswal.io
In ICSE Class 10 Mathematics, Chapter 17 focuses on “Mensuration.” This chapter deals with the measurement of geometric figures, such as areas and volumes. It is an essential part of mathematics as it helps students understand and calculate the sizes and capacities of various shapes and objects.

Introduction

In Class 10 ICSE (Indian Certificate of Secondary Education) mathematics, the chapter on “Mensuration” is a fundamental topic that deals with the measurement of geometric figures, including calculating their areas and volumes. Mensuration is a practical and essential part of mathematics with numerous real-world applications. Mensuration is not just a mathematical concept; ICSE class 10 maths mensuration is a practical tool that helps us quantify and measure objects in our everyday lives. Whether you’re designing a building, calculating the area of a land plot, or estimating the volume of a container, mensuration plays a vital role in solving real-world problems accurately. Here are some area and volume class 10 ICSE questions.

What is Mensuration?

Mensuration is the branch of mathematics that focuses on measuring the sizes, areas, and volumes of various geometric shapes and figures. ICSE class 10 maths mensuration provides us with the tools and formulas to quantify and understand the spatial properties of objects in both two and three dimensions.
Key Concepts and Objectives:
Area and Perimeter: Mensuration helps us calculate the area (space inside a shape) and perimeter (the boundary length) of 2D figures such as rectangles, squares, circles, and triangles.
Volume: It allows us to determine the volume (space occupied) of 3D figures like cubes, cuboids, cylinders, cones, and spheres.
Formulas: Mensuration provides us with specific formulas and methods for each type of shape, making it possible to compute measurements accurately.
area and volume class 10 icse questions

Class 10 Mensuration Important Questions and Answers

Q1. Volume of a cone is 220 cm^3. The volume of the cylinder having same radius and height as that of the given cone is:
Options
(a) 220 cm^3\\ (b) 110 cm^3 \\ (c) 660 cm^3 \\ (d) 330 cm^3

Ans. (C) 660 cm^3 \\ Explanation:
volume of cone = (1/3) πr^2h = 220 cm^3 \\ \text{Volume of cylinder} = πr^2h = 3×220 cm^3 \\ (∵ radius and height of cylinder are as same as that of cone)

Q2. If the circumference of a circle and the perimeter of a square are equal then:
Options
(a) area of the circle = area of the square
(b) area of the cricle > area of the square
(c) area of the circle < area of the square
(d) none of these

Ans. (b)
Explanation:
Circumference of circle = 2πR Perimeter of square = 4a
According to question  2πR = 4a
⇒ πR = 2a
⇒ \frac{\pi R}{2} = a \\ \text{Area of square =} a^2 \\ = \left(\frac{\pi R}{2}\right )^2 \\ =\frac{\pi^2 R^2}{4} \\ \begin{bmatrix} \because \pi = 3.14 \space \space and \space \space 3.14 \lt 4 \\ \therefore \frac{3.14}{4}\lt 1\end{bmatrix} \\ π R^2> \frac{\pi}{4} π R^2 \\ Area of circle > Area of square

Q3. Determine :
(i) The curved or lateral surface area of a cylindrical petrol storage tank that is 4·0 m in diameter and 4·4 m high.
(ii) How much steel was actually used, if \space \frac{1}{2} \space of the steel actually used was wasted in making the closed tank.

Explanation:
(i) Here,
r= \frac{4.0}{2} = 2m \space and \space h = 4⋅4 m \\ \text{Curved surface area =} 2πrh m^2 \\ =2× \frac{22}{7} ×2×4⋅4 cm^2 \\ = 55.31 m^2 \\ (ii) Since \frac{1}{2} of the actual steel used was wasted, the area of the steel which has gone into the tank = \begin{pmatrix}1- \frac{1}{12}\end{pmatrix} = \frac{11}{12} of x, where
x = total area of steel used . Steel used = (2πrh + 2πr^2) m^2 \\ =(55⋅31+2× \frac{22}{7} ×4) m^2 \\ = (55·31 + 25·14) m^2‍ \\ = 80·45 m^2 \\ ∴ \frac{11}{12}x =80.45 \\ ⇒  x = 87·76 m^2 \\ Hence, the actual area of the steel used = 87·76 m^2.

Q4. A circus tent is cylindrical to a height of 3 metres and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas which is 5 m wide to make the required tent.

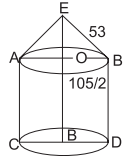
Explanation:
Cylindrical area=2πrh
= 2 × \frac{22}{7} × \frac{105}{2} ×3 m^2 \\ = and conical area = πrl
=\frac{22}{7} × \frac{105}{2} × 53 m^2

Mensuration_Q4
=2× \frac{22}{7} × \frac{105}{2} x 3 + \frac{22}{7} × \frac{22}{7} × \frac{105}{2} × 53 \\ =15×11(2×3+53) \\ =15×11×59 \\ =165×59 m^2 \\ \text{Length of canvas =}\frac{165×59}{5}m\\ =33×59 m
=1947 m.

Q5. A circus tent consists of cylindrical base surmounted by a conical roof. The radius of the cylinder is 10 m. The height of the tent is 60 m and that of the cone is 20 m. Find the volume of the tent and the area of the canvas used for making it.

Explanation:
Height of the tent = Height of cone + Height of the cylinder

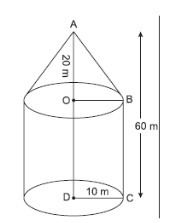
Mensuration_Q5

Given, height of tent = 60 m
H = height of cone = 20 m
∴ Height of cylinder             
= h = 60 – 20 = 40 m
and Radius of cone = Radius of cylinder                              r = 10 m
∴ Volume of the tent = Volume of cylinder+ Volume of the cone=πr^2h + \frac{1}{3} πr^2H \\ = πr^2 \begin{pmatrix}h+ \frac{H}{3}\end{pmatrix} \\ = π(10)^2 \begin{pmatrix}  40+ \frac{20}{3}\end{pmatrix} \\ =100 × \frac{22}{7} \begin{pmatrix}\frac{140}{3}\end{pmatrix} \\ = 14666·6 m^3 \\ Slant height of the cone is I= \sqrt{H^2+r^2} \\ = \sqrt{400+100} \\ = \sqrt{500} = \sqrt[10]{5} m Since, curved surface area of cone= πrl 
= \frac{22}{7} ×10×10 \sqrt{5} m^2 and curved surface area of cylinder
= 2πrh=2× \frac{22}{7} ×10×40 ∴ Total surface area of the canvas in making the tent
= C.S.A. of cylinder + C.S.A. of cone
= 2πrh + πrl
= πr (2h + l)
= \frac{22}{7} ×10(2×40+10 \sqrt{5})m^2\\ = \frac{220}{7} (80+10 \sqrt{5})m^2\\ \text{Total Surface Area =} 3217·04 m^2

Want to Master this Chapter?
Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Download Now

Want to Practice Mock Tests of this chapter

Practice Now

Download Important Questions of this chapter

Download Now
Want to Master this Chapter?
Our Practice Tests, Mind Maps, and Key Questions will help!
Download Mind Map of this chapter
Download Now
Want to Practice Mock Tests of this chapter
Practice Now
Download Important Questions of this chapter
Download Now

ICSE Class 10 Maths Chapter wise Important Questions

Chapter No.Chapter Name
Chapter 1Goods and Service Tax (GST)
Chapter 2Banking
Chapter 3Shares and Dividends
Chapter 4Linear inequations
Chapter 5Quadratic Equations in one variable
Chapter 6Ratio and proportion
Chapter 7Factorization
Chapter 8Matrices
Chapter 9Arithmetic Progression
Chapter 10Geometric Progression
Chapter 11Coordinate Geometry
Chapter 12Reflection
Chapter 13Similarity
Chapter 14Loci
Chapter 15Circles
Chapter 16Constructions
Chapter 17Mensuration
Chapter 18Trigonometry
Chapter 19Statistics
Chapter 20Probability

Conclusion

In conclusion, the chapter on ICSE class 10 maths mensuration is an integral part of the curriculum, offering students the essential knowledge and skills to measure and calculate areas and volumes of geometric shapes. These concepts extend far beyond the classroom, finding application in various real-world scenarios such as construction, design, and everyday problem-solving. Mastery of mensuration equips students with a valuable toolkit for understanding and quantifying the spatial attributes of objects, laying the foundation for more advanced mathematical concepts and practical life applications. If you want to get better at this chapter and really understand it, check out oswal.io. They have lots of extra questions to help you practice and get a deeper grasp of the ideas. It’s like having a treasure chest of knowledge to make you a math wizard!

Frequently Asked Questions

Ans: Mensuration in mathematics is the study of measuring and calculating the areas and volumes of geometric shapes and figures.
Ans: Mensuration is crucial because it helps us quantify and understand the sizes of objects in real-world situations, including construction, design, and everyday problem-solving.
Ans: Common 2D shapes include rectangles, squares, circles, triangles, and parallelograms.
Ans: The area of a rectangle is calculated by multiplying its length and width (A = length × width).
Ans: The perimeter of a square is four times the length of one of its sides (P = 4 × side length).
logo
Instagram Linkedin-in Facebook-f Youtube Twitter
logo
Instagram Linkedin-in Facebook-f Youtube Twitter

CBSE Important Questions Class 10

ICSE Important Questions Class 10

CBSE Important Questions Class 10

ICSE Important Questions Class 10

Contact Us

© Copyright 2025 oswal.io by
Oswal Publishers Simplifying Exams