Class 10 Maths Chapter 14
Loci
Important Questions

Chapter 14 of ICSE Class 10 Mathematics, titled "Loci," takes students on a journey into the realm of geometry and constraints. This chapter introduces the concept of loci, which involves exploring the paths or positions that points or objects can occupy based on specific conditions or constraints. Here's an introductory overview of Chapter 14 - "Loci," along with some important questions:

"In Chapter 14, 'Loci,' of ICSE Class 10 Mathematics, students embark on a captivating exploration of geometric constraints and possibilities. Loci, the central theme of this chapter, invites students to discover the fascinating paths and positions that points or objects can assume when guided by particular conditions or rules.

Introduction

Chapter 14 Loci of class 10 ICSE Mathematics, titled "Loci," offers students a captivating exploration into the world of geometric constraints and the boundless possibilities they present. This chapter introduces the concept of loci, which involves the art of identifying and comprehending the specific paths, positions, or regions that points or objects can take on, guided by particular conditions or constraints. 
"In ICSE Class 10 Mathematics, Chapter 14, 'Loci,' invites students on a captivating journey through the realm of geometry and its intriguing constraints. Loci takes center stage in this chapter, beckoning students to delve into the fascinating routes and positions that points or objects may traverse when governed by precise rules or conditions.

What is Loci?

In Loci of class 10 ICSE  Mathematics, "Loci" refers to the set of all points that satisfy specific geometric conditions or constraints. Essentially, it represents the path, position, or region that a point or object can occupy based on certain rules or limitations within the context of geometry. 
‍
Loci are used to describe and analyze relationships between points, lines, and shapes in geometry. They help in solving problems that involve constraints and conditions.
‍
Loci can be represented as curves, lines, or shapes on a plane, depending on the nature of the geometric conditions.
‍
Geometric Conditions: Loci are defined by specific geometric conditions, such as distances, angles, or relationships between points or objects.
‍
Representation: A locus can be represented as a collection of points or as a curve, line, or shape on a plane, depending on the nature of the conditions.

Class 10 Loci Important Questions and Answers

Q1.  For all the value of co-ordinates of a moving point Q are (a cos q, b sin q), then the equation of the locus of Q is:

Options

(a) \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2}\) = 1
(b) \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2}\) = 0
(c) \(\dfrac{x^2}{b^2} + \dfrac{y^2}{a^2}\) = 0
(d) \(\dfrac{x^2}{b^2} + \dfrac{y^2}{a^2}\) = 1

Ans. (a)\(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2}\) = 1

Explanation:
Let (x, y) be the coordinates of any point on themoving point Q.
Then we shall have
X = a cos θ or \(\dfrac{x}{a}\) = cos θ
X = b sin θ or \(\dfrac{y}{b}\) = sin θ
⇒ \(\dfrac{x^2}{a^2}\) + \(\dfrac{y^2}{b^2}\) = 1
[∵ sin² + cos² θ =1]

Q2. The locus of a point a moving in a plane about another point ‘b’ in such a way that its distance from it is constant is called:

Options

(a) Axe
(b) Circle
(c) Angle
(d) None of these

Ans. (b) Circle

Explanation:
According to locus postulate.

Q3. Prove that the common chord of two intersecting circles is bisected at right angles by the line of centers. 

Explanation:
Given, two intersecting circles with centers C and D.
AB is their common chord. 
To prove : AB bisected by CD at right angles.

Proof : CA = CB (radii)
∴ C lies on the right bisector of AB. Similarly, D lies on the right bisector of AB. 
Therefore, CD is the right bisector of AB.

Q4.  The bisector of ∠B and ∠C of a quadrilateral ABCD intersect in P, show that P is equidistant from the opposite sides AB and CD.

Explanation:
Given, in quadrilateral ABCD, bisectors of ∠ B and ∠C meet in P. PM ⊥ AB and PN ⊥ CD. To prove that: 
PM = PN   …(i)
Construction: Draw PL ⊥ BC
Proof : P lies on bisector or of  ∠B

∴ PM = PL
‍P lies on bisector of ∠C
PL = PN        …(ii) 
From (i) and (ii), we have
PM = PN.

Q5. Construct a triangle ABC with AB = 5·5 cm, AC = 6 cm and ∠ BAC = 105°. Hence
(i) Construct the locus of points equidistant from BA and BC.
(ii) Construct the locus of points equidistant from B and C.
(iii) Mark the point which satisfies the above two loci as P. Measure and write the length of PC.

Explanation:
Steps of construction :
(i) Draw a line AB = 5·5 cm.
(ii) Now, from point A draw ∠ XAB = 105°.
(iii) Taking A as centre and 6 cm as radius drawarc on AX mark this point as C.
(iv) Join BC.
(v) Draw bisector of ∠ ABC and perpendicularbisector of BC, both intersecting at P. P isthe required point.

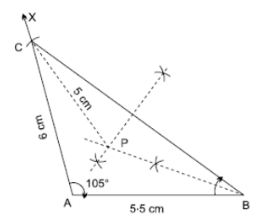
Reason :
Since, (i) P is on bisector of angle ABC, P is equidistant from BA and BC.
(ii) P is on perpendicular bisector of BC, P is equidistant from B and C.
(iii) Length of PC is 5 cm.

ICSE Class 10 Maths Chapter wise Important Questions

Conclusion

In Loci of class 10 ICSE Mathematics, the topic of loci is an important concept in geometry. Loci refers to the set of points that satisfy a certain condition or constraint. Loci concepts have practical applications in fields like engineering, architecture, navigation, and computer graphics. They help in designing structures and solving real-world problems. If you want to get better at this chapter and really understand it, check out oswal.io. has lots of class 10 Mensurations important questions and answers to help you practice and get a deeper grasp of the ideas.

Frequently Asked Questions

Q1 : What is a locus in geometry?

Ans: A locus is a set of points that satisfies a specific geometric condition or constraint.

Q2: How do you define the locus of points equidistant from two fixed points?

Ans:  The locus of points equidistant from two fixed points is the perpendicular bisector of the line segment connecting those two points.

Q3 : What is the locus of points at a fixed distance from a given line?

Ans: The locus of points at a fixed distance from a given line is a pair of parallel lines that are equidistant from the given line.

Q4 : How do you find the locus of points making a certain angle with a given line?

Ans: The locus of points making a certain angle (θ) with a given line is a pair of lines that form an angle of θ with the given line.

Q5 : What is the locus of points that are equidistant from three non-collinear points?

Ans: The locus of points equidistant from three non-collinear points is the circumcircle of the triangle formed by those three points.