logo
Log in
  Get Rs 200 off on Oswal Premium Plan for your board preperatoin! For Class 9th till 12th. Use Coupon Code BOARD200 at checkout.
logo
Log in
Start Free Trial
Banking

Home / Board / ICSE / important Questions / Class 10 / Maths / Banking

Class 10 Maths Chapter 2
Banking
Important Questions

exam preparation with oswal.io
Class 10 Mathematics Chapter 2 ‘Banking’ is an important topic that requires thorough understanding and practice.This chapter is like your secret vault, filled with mathematical treasures that will make you a financial wizard. Within these pages, you’ll find important questions that are like magical keys. They unlock the secrets of interest, rates, and the art of making money work for you. These questions are your ticket to understanding how banks function and how you can make smart financial choices. As you delve into banking class 10 ICSE questions, you’ll learn how to calculate interest effortlessly, decipher the mysteries of principal, rate, and time, and discover how math plays a vital role in everyday financial decisions.

Introduction

Imagine a world where money lies stagnant, unable to grow or work for you. That’s why icse class 10 maths banking chapter is incredibly important. It’s your key to unraveling the financial forces that shape our modern world. In this chapter, you become a financial detective, diving into the world of interest rates, loans, and investments. Banking is more than just handling money; it’s about making your money a dynamic force. These mathematical ideas of banking class 10 ICSE questions, aren’t just for exams; they’re life skills that empower you to thrive in the real world.

What is Banking?

“Banking” in icse class 10 maths banking typically refers to the concept of compound interest. Compound interest is a fundamental topic in mathematics related to finance and banking. It involves the process of earning interest not only on the initial amount of money deposited or borrowed (the principal) but also on any interest that has already been earned or charged. This results in the exponential growth of the principal amount over time.
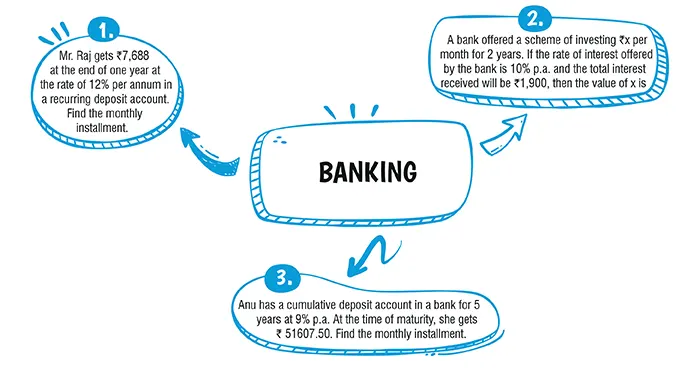
icse class 10 maths banking important questions

Class 10 Banking Important Questions and Answers

Q1. Mr. Raj gets ₹ 7,688 at the end of one year at the rate of 12% per annum in a recurring deposit account. Find the monthly installment.
Options
(a) ₹ 500
(b) ₹ 600
(c) ₹ 700
(d) ₹ 800

Ans. (a) ₹ 600
Explanation:
MV=P×n+P×\frac{n(n+1)}{2×12}×\frac{r}{100} \\ \Rightarrow 7,668=P\begin{pmatrix} 12+\frac{12×(12+1)}{2×12}×\frac{12}{100}\end{pmatrix} \\ \left[\because n=1 \space \displaystyle{year}=12\space \displaystyle{months} \right] \\ ⇒ 7,668=P\begin{pmatrix} 12+\frac{78}{100}\end{pmatrix} \\ \Rightarrow 7,668=P\begin{pmatrix} 12+\frac{1,278}{100}\end{pmatrix}\\ ⇒ P = 600

Q2. A bank offered a scheme of investing ₹ x per month for 2 years. If the rate of interest offered by the bank is 10% p.a. and the total interest received will be ₹ 1,900, then the value of x is
Options
(a) ₹ 700
(b) ₹ 750
(c) ₹ 760
(d) ₹ 800

Ans. (d) ₹ 760

Explanation:
we have 
P = ₹ x, n=2 years = 24 months, r = 10% and 
I = ₹ 1,900
We know,
I = P × \frac{n(n+1)}{2×12}×\frac{r}{100} \\ ⇒  1,900 \\ = x × \frac{24×25}{24} × \frac{10}{100}\\ ⇒  1,900 =  2.5 x
⇒  x = 760.

Q3. Mohan has a recurring deposit account in a bank for 2 years at 6% p.a. simple interest. If he gets  ₹ 1200 as interest at the time of maturity, find :
(a) the monthly installment
(b) the amount of maturity.

Explanation:
(a) Since, number of months (n) = 24 and rate of interest (r) = 6%
I = P ×\frac{n(n+1)}{2×12} × \frac{6}{100} \\ ⇒ 1200 = P × \frac{24(24+1)}{2×12} × \frac{6}{100} \\ ⇒  P = \frac{24(24+1)}{2×12} × \frac{6}{100}\\ = ₹ 800
∴ Monthly instalment = ₹ 800 Ans.
(b) Sum deposited = ₹ 800 × 24
= ₹ 19200
Amount on maturity = ₹ 19,200 + ₹ 1,200
= ₹ 20,400 Ans.

Q4. Anu has a cumulative deposit account in a bank for 5 years at 9% p.a. At the time of maturity, she gets ₹ 51607.50. Find the monthly installment.

Explanation:
we have,
n = 5 year = 5 × 12 = 60 months, r = 9% M.V. = ₹ 51607.50.
Since,
I = P× \frac{n(n+1)}{2×12} × \frac{r}{100} \\ = P × \frac{60×61}{2×12} × \frac{9}{100} \\ = \frac{549P}{40} \\ ∴ M.V. = Pn + I \\ = P  × 60+ \frac{549P}{40} \\ = \frac{2400+549P}{40} \\ = \frac{2949P}{40} \\ \text{According to the question,} \\ =\frac{2949P}{40} \\ = 51607.50 \\ ⇒ P =\frac{51607.50×40}{2949} ∴ P = ₹ 700.

Q5. Government-owned banks have security assured over the investments made by the customers, while private banks provide better services and rate of interest to attract customers. A retired manager from Punjab National Bank, Mr Ranajit Bhattacharya invests in a recurring deposit scheme in IDBI bank with ₹ 10000/-for 6 years and receives ₹ 8,84,250/-. His friend Lt. Colonel Jayant Paranjpe invested in a similar recurring deposit scheme with Punjab National Bank with ₹ 10000/-for 6 years and receives ₹ 19,710/- less than Mr Ranajit Bhattacharya. What is the difference between the respective rates of interest of the two banks?

Explanation:
Here we have Ranajit Bhattacharya.
P = ₹ 10000, time = 6 years 6 × 12 = 72 months and we have to find r%
Clearly,
MV = P × n + P ×\frac{(n)(n+1)}{2×12} × \frac{r}{100} \\ \text{(i) so that we get.} \\ 8,84,250 = ₹ 10000 × 72 + \frac{(72)(78)}{24} × \frac{r}{100}, \\ on solving we get: r% = 7.4%
Now for Lt Colonel Jayant:
P = ₹ 10000, time = 6 years 6 × 12 = 72 months and we have to find r% His maturity value is ₹ 19.710 less than the maturity value of Mr Ranajit:
I.e. ₹ 8,84,250 - ₹ 19.710 = ₹ 8,64,540 and rate is not known. Let it be R%
Clearly, ₹ 8,64,540
= ₹ 10,000 × 72 + = ₹ 10000 × \frac{(72)(78)}{24}×\frac{R}{100}, \\ on solving for R We get: R% = 6.6%
So the difference between the rate% = 7.4%- 6.6% = 0.8% Ans.

Want to Master this Chapter?
Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Download Now

Want to Practice Mock Tests of this chapter

Practice Now

Download Important Questions of this chapter

Download Now
Want to Master this Chapter?
Our Practice Tests, Mind Maps, and Key Questions will help!
Download Mind Map of this chapter
Download Now
Want to Practice Mock Tests of this chapter
Practice Now
Download Important Questions of this chapter
Download Now

ICSE Class 10 Maths Chapter wise Important Questions

Chapter No.Chapter Name
Chapter 1Goods and Service Tax (GST)
Chapter 2Banking
Chapter 3Shares and Dividends
Chapter 4Linear inequations
Chapter 5Quadratic Equations in one variable
Chapter 6Ratio and proportion
Chapter 7Factorization
Chapter 8Matrices
Chapter 9Arithmetic Progression
Chapter 10Geometric Progression
Chapter 11Coordinate Geometry
Chapter 12Reflection
Chapter 13Similarity
Chapter 14Loci
Chapter 15Circles
Chapter 16Constructions
Chapter 17Mensuration
Chapter 18Trigonometry
Chapter 19Statistics
Chapter 20Probability

Conclusion

Goods and Services Tax (GST) is a fundamental topic within the ICSE Class 10 Mathematics curriculum and carries substantial relevance in practical scenarios. It represents a consolidated tax system implemented in India to streamline and simplify the taxation framework by replacing a multitude of indirect taxes. If you seek additional practice and a deeper comprehension of the topics covered in the chapter, oswal.io offers an extensive array of questions on important questions on gst class 10 ICSE 2024 to facilitate a more profound understanding of the concepts.

Frequently Asked Questions

Ans: Simple interest is calculated only on the initial principal amount, while compound interest takes into account both the principal and the accumulated interest.
Ans:  Simple Interest (SI) can be calculated using the formula: SI =\frac{P.R.T}{100}, \\ where P is the principal amount, R is the rate of interest, and T is the time in years.
Ans: The nominal interest rate is the stated interest rate, while the effective interest rate takes into account the compounding frequency. It is the actual rate at which interest is earned or paid.
Ans: The total amount (A) with annual compounding can be found using the formula: A= P(1 +\frac{R}{100})^T
Ans: Compound Interest (CI) is calculated using the formula: A= P(1 +\frac{R}{100})^T-P,\\ where A is the final amount, P is the principal, R is the rate of interest, and T is the time in years.
logo
Instagram Linkedin-in Facebook-f Youtube Twitter
logo
Instagram Linkedin-in Facebook-f Youtube Twitter

CBSE Important Questions Class 10

ICSE Important Questions Class 10

CBSE Important Questions Class 10

ICSE Important Questions Class 10

Contact Us

© Copyright 2025 oswal.io by
Oswal Publishers Simplifying Exams