Table of Contents
Ans.(b) 9 cm
Explanation:
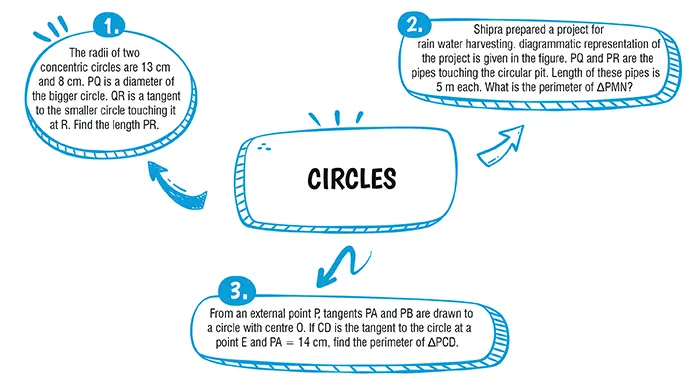
Since, PA and PB are tangents to the circle from point P.
Therefore PA = PB …(i)
Also, CD is the tangent touching the circle at Q.
Therefore, CA = CQ and DQ = DB …(ii)
Since, tangents from external points are equal.
Now, PA = PB = 12 cm
CA = CQ = 3 cm
PC = PA - CA
= 12 - 3 = 9 cm.
Ans. (b) 2 cm
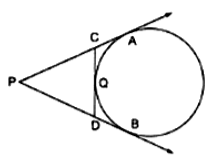
Explanation:
An incircle is drawn with centre O which touches the sides of the triangle ABC at P, Q and R. OP, OQ and OR are radii and AB, BC and CA are the tangents to the circle.
OP ⊥ AB, OQ ⊥ BC and OR ⊥ CA.
OPBQ is a square. ( ∵ ∠B - 90^o)\\
Let r be the radius of the circle
PB = BQ = r
AR = AP = 8 - r,
CQ = CR = 6 - r
AC = AR + CR
⇒ 10 = 8 - r + 6 - r
⇒ 10 = 14 - 2r
⇒ 2r = 14 - 10 = 4
⇒ r = 2
∴ Radius of the incircle = 2 cm.
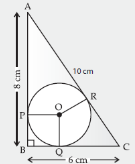
Explanation:
Let the line QR intersect the bigger circle at S.
Join PS.
O is the mid-point of PQ. [∵ PQ is a diameter of the bigger circle]
QR is a tangent to the smaller circle and OR is a radius through the point of contact R.
∴ OR ⊥ QR ⇒ OR ⊥ QS
Since, OR is perpendicular to a chord QS of the bigger circle.
∴ QR = RS
[ ∵ Perpendicular from the centre to a chord bisects the chord]
⇒ R is the mid - point of Qs.
∴ In △QSP, O is the mid-point of PQ and R is the mid-point of QS. \\\text{OR} = \dfrac{1}{2} \text{Ps} \\
[∵ segment joining the mid-points of any two sides of a triangle is half of the third side]
⇒ PS = 2OR = 2 × 8 cm = 16 cm
\\
\text{In right △OQR, OR}^2 + QR^2 = OQ^2\\[4.5 bp]
⇒ 8^2 + QR^2 = 13^2\\[4.5 bp]
⇒ 64 + QR^2 = 169\\[4.5 bp]
⇒ QR^2 = 169 – 64 = 105 \\[4.5 bp]
QR = \sqrt{105} \\[4.5 bp]
\therefore \space RS = QR = \sqrt{105}\\[4.5 bp]
\text{In △PRS, PR}^2 = \text{RS}^2\text{ + PS}^2\\[4.5 bp]
= (\sqrt{105})^2 + 16^2\\[4.5 bp]
⇒ PR = 19\space cm.
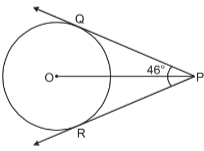
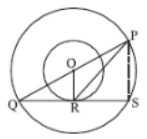
Explanation:
Join OP, such that it bisects ∠QPR.
Thus, ∠OPQ = ∠OPR = 23°
Also, ∠OQP = ∠ORP = 90°
So, ∠QOP = ∠ROP
= 180° – (90° + 23°)
= 180° – 113° = 67°
Hence, ∠QOR = ∠QOP + ∠ROP
= 67° + 67°
= 134°
Explanation:
Given, PA and PB are the tangents drawn from a point P outside the circle with centre O.
CD is another tangent to the circle at point E which intersects PA and PB at C and D respectively.
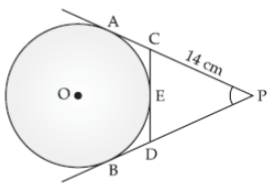
Here, PA = 14 cm
PA and PB are the tangents to the circle from P
So, PA = PB = 14 cm
Now, CA and CE are the tangents from C to the circle.
∴ CA = CE …(i)
Similarly , DB and DE are the tangents from D to the circle.
∴ DB = DE …(ii)
Now, perimeter of △PCD
= PC + PD + CD
= PC + PD + CE + DE
= PC + CE + PD + DE
= PC + CA + PD + DB
{From (i) and (ii)}
= PA + PB
= 14 + 14
= 28 cm
| Chapter No. | Chapter Name |
|---|---|
| Chapter 1 | Real Numbers |
| Chapter 2 | Polynomials |
| Chapter 3 | Pair of Linear Equations in Two Variable |
| Chapter 4 | Quadratic Equations |
| Chapter 5 | Arithmetic Progressions |
| Chapter 6 | Triangles |
| Chapter 7 | Coordinate Geometry |
| Chapter 8 | Introduction to Trigonometry |
| Chapter 9 | Some Applications of Trigonometry |
| Chapter 10 | Circles |
| Chapter 11 | Areas Related to Circle |
| Chapter 12 | Surface Areas and Volumes |
| Chapter 13 | Statistics |
| Chapter 14 | Probability |
| Chapter Wise Important Questions for CBSE Board Class 10 Maths |
|---|
| Real Numbers |
| Polynomials |
| Pair of Linear Equations in Two Variables |
| Quadratic Equations |
| Arithmetic Progressions |
| Triangles |
| Coordinate Geometry |
| Introduction to Trigonometry |
| Some Applications of Trigonometry |
| Circles |
| Areas Related to Circles |
| Surface Areas and Volumes |
| Statistics |
| Probability |
CBSE Important Questions Class 9
CBSE Important Questions Class 10
CBSE Important Questions Class 12
CBSE Practice Papers
CBSE Practice Papers
ICSE Important Questions Class 9
ICSE Important Questions Class 10
ICSE Practice Papers
ISC Important Questions Class 12
ISC Practice Papers
Contact Us
CBSE
Important Questions
Class 10
Maths
Science
Social Science
English
Chemistry
Biology
Physics
Computer Applications
History & Civics
Geography
Business Studies
Economics
Accountancy
Political Science
General Test
