Geometric Progression

Home / Board / ICSE / important Questions / Class 10 / Maths /Geometric Progression

Class 10 Maths Chapter 10
Geometric Progression
Important Questions

Q: Q1. What is a Geometric Progression (GP)?

Ans: A GP is a sequence of numbers in which each term is obtained by multiplying the preceding term by a constant non-zero number called the common ratio.

Q: Q2. How is the common ratio (r) of a GP calculated?

Ans: The common ratio (r) is calculated by dividing any term in the GP by its preceding term: \\ r = \frac{a_n}{a_n – 1}

Q: Q3. What is the formula for the nth term of a GP?

Ans: The nth term of a GP is given by: \\ a_n = a.r^{\left(n – 1\right)}

Q: Q4. How do you find the sum of the first 'n' terms of a GP?

Ans: The sum of the first ‘n’ terms of a GP is calculated using the formula: \\ S_n = \frac{a(r^n – 1)}{r – 1}.

Q: Q5. What happens if the common ratio (r) is greater than 1 in a GP?

Ans: If r is greater than 1, the GP is increasing, and the terms become larger as the sequence progresses.

Some important questions related to Chapter 10 – Geometric Progression in ICSE Class 10 Mathematics. These questions cover various concepts and can help you prepare for your exams. Remember to solve these questions and practice other exercises from your textbook to thoroughly understand the topic. We’ve put together a collection of essential geometric progression class 10 ICSE questions specifically focused on Class 10 Geometric Progression. These questions serve as a valuable resource to bolster students’ mathematical proficiency, address any uncertainties they may have, and conquer potential challenges encountered during their study of this topic. By working through these questions, students can fortify their understanding of this fundamental mathematical concept, ultimately equipping themselves to excel in their Class 10 Mathematics examinations.

Table of Contents

Introduction

In chapter 10 of Class 10 Mathematics, Geometric Progression ICSE Mathematics, students are introduced to the concept of a Geometric Progression (GP), also known as a Geometric Sequence. A Geometric Progression is a fundamental mathematical sequence with a unique pattern. It is defined as a sequence of numbers where each term is found by multiplying the preceding term by a constant number called the “common ratio.” Here’s an introductory explanation of a Geometric Progression for Class 10 students: A Geometric Progression (GP) is a sequence of numbers that follows a specific multiplication pattern. In a GP, each term is obtained by multiplying the previous term by the same fixed number, known as the “common ratio.” This common ratio is represented by the letter “r.” The general form of a Geometric Progression looks like this:

a, ar, ar_2, ar_3, ar_4,

… Where: “a” is the first term of the sequence. “r” is the common ratio.

What is Geometric Progression?

A Geometric Progression (GP) as we study in geometric progression class 10 ICSE is a sequence of numbers where each number is found by multiplying the previous one by the same amount. This special amount we multiply by is called the “common ratio.” Imagine you have a starting number, let’s call it “a.” Then, to find the next number in the sequence, you don’t add or subtract like in some other sequences. Instead, you multiply “a” by a fixed number “r” to get the next number, and you keep doing this for all the numbers in the sequence. So, if “a” is 2, and “r” is 3, our GP would look like this: 2, 6, 18, 54, 162, … Here’s a breakdown of the terms: The first term is 2 (that’s just our starting number). To get the second term, we multiply the first term (2) by the common ratio (3), so we get 2 * 3 = 6. To find the third term, we multiply the second term (6) by the common ratio (3) again, giving us 6 * 3 = 18. We keep doing this for each term in the sequence.

Class 10 Geometric Progression Important Questions and Answers

Q1. The 11th term of the G.P.

$\frac{1}{8},\frac{-1}{4} ,2,-1,....is$

Options

(a) 18
(b) 19
(c) 20
(d) 21

Ans. (c) 20
Explanation:
$\text{11th term of the G.P.} \\ \frac{1}{8},\frac{-1}{4} ,2,-1,....is \\ \text{Here, First term} (a)=\frac{1}{8} \\ \text{Common ratio} (r)= \frac{-1}{4} ÷ \frac{1}{8} \\ = \frac{-1}{4} × \frac{8}{1} =-2 \\ =-\frac{1}{4}×8=--2 \\ 11^{th} term of G.P.=a^{11} a^{11} = ar^{n-1} \\ = \frac{1}{2^3} × (–1)^{10} × 2^{10} =1×2^{10-3} \\ =2^7 \\$ =128.

Q2. The list of number.

$\frac{1}{9},\frac{1}{3},1,-3…. Is a$

Options

(a) G.P. with r = – 3
(b) G.P. with r = – 1/3
(c) G.P. with r = 3
(d) not a G.P.

Ans. (c)
Explanation:
$\frac{1}{9},\frac{1} {3},1,-3....Here,\\ \text{Firstterm (a)} = \frac{1}{9} = \frac{-1}{3} ÷ \frac{1}{9} = \frac{-1}{3} = 9 = - 3 \\$ It is a G.P. with r = – 3.

Q3. The sum of first three terms of a G.P. is 16 and the sum of next three terms is 128. Determine the sum of n terms of the G.P.

Explanation:
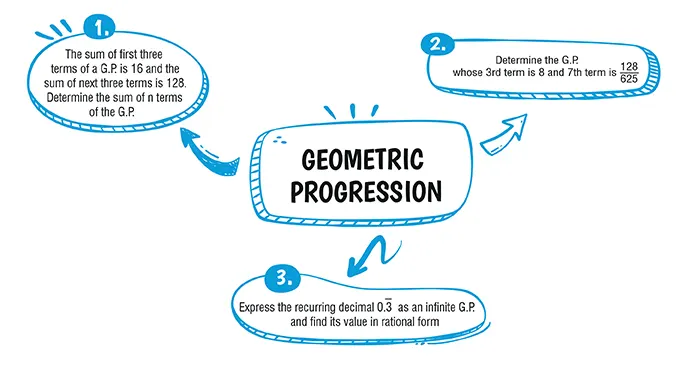
Let a be the first term and r be the common ratio of the G.P. Then, according to given condition,
$a + ar + ar^2 = 16 …(i)\\ and \space \space ar^3 + ar^4 + ar^5 = 128 …(ii) \\ ⇒ a (1 + r + r^2) = 16 \space and \space ar^3 (1 + r + r^2) = 128 \\ ⇒ \frac{ar^3(1+r+r^2)}{a(1+r+r^2)}\\ = \frac{128}{16} \\ ⇒ r^3 = 8 \\$ ⇒ r = 2 Putting r = 2 in equation (i),
we get
a + 2a + 4a = 16
⇒ 7a = 16
$⇒ a = \frac{16}{7}\\ ∴ \text{Sum of n terms,}\space Sn = \frac{a(r-1)}{r - 1} \\ ⇒ S_n = \frac{16}{7}\\ \left(\frac{2^n – n}{2 – 1} \right)\\ =\frac{16}{7}(2n-1)$

Q4. Determine the G.P.

whose 3rd term is 8 and 7th term is $\frac{128}{625}$

Explanation:
Given:
$a^3 = 8 \space and \space a^7 = \frac{128}{625} \\$ Let a, ar, $ar^2$ , …… be the G.P.
Then, $a^3 = ar^2 \space and \space a^7 = ar^6 \\ \text{Now,}\\ \frac{a_7}{a_3} = \frac{ar^6}{ar^2} = r^4 \space \text{and} \space \frac{a_7}{a_3} = \frac{128}{625×8} = \frac{16}{625} \\ ∴ r^4 = \frac{16}{625} = \begin{pmatrix} \frac{2}{5}\end{pmatrix}^4 \\ \Rightarrow r = ± \frac{2}{5} \\ \space As \space ar^2 = 8a = 8 × \begin{pmatrix} \frac{5}{2}\end{pmatrix}^2 \\ =\frac{8×25}{4} = 50 \\$ ∴ G.P. is 50, 20, 8, …… (when r = 2/5).
or 50, – 20, 8, …… (when r = – 2/5).

Q5. Express the recurring decimal 0.3 as an infinite G.P. and find its value in rational form.

Explanation:
$0.\={3} =0⋅3333333… \\ =0⋅3+0⋅03+0⋅003+0⋅0003+... \\ =\frac{3}{10} + \frac{3}{10^2} + \frac{3}{10^3} + \frac{3}{10^4} + \text{.........The above is an infinite G.P.} \\ \text{with the first term a} = \frac{3}{10} \space and \space r = \frac{\frac{3}{10^2}}{\frac{3}{10}} = \frac{1}{10}<1 \\ \text{Hence, by using the formula} S= \frac{a}{1-r},\\ \text{we get}\\ 0. \={3} = \frac{\frac{3}{10}}{1-\frac{1}{10}} = \frac{\frac{3}{10}}{\frac{9}{10}} = \frac{3}{9} = \frac{1}{3} \\ \text{Hence, the recurring decimal}\\ 0.\={3} = \frac{1}{3}.$

Want to Master this Chapter?

Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Download Now

Want to Practice Mock Tests of this chapter

Practice Now

Download Important Questions of this chapter

Download Now

Want to Master this Chapter?

Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Want to Practice Mock Tests of this chapter

Download Important Questions of this chapter

ICSE Class 10 Maths Chapter wise Important Questions

Chapter No.	Chapter Name
Chapter 1	Goods and Service Tax (GST)
Chapter 2	Banking
Chapter 3	Shares and Dividends
Chapter 4	Linear inequations
Chapter 5	Quadratic Equations in one variable
Chapter 6	Ratio and proportion
Chapter 7	Factorization
Chapter 8	Matrices
Chapter 9	Arithmetic Progression
Chapter 10	Geometric Progression
Chapter 11	Coordinate Geometry
Chapter 12	Reflection
Chapter 13	Similarity
Chapter 14	Loci
Chapter 15	Circles
Chapter 16	Constructions
Chapter 17	Mensuration
Chapter 18	Trigonometry
Chapter 19	Statistics
Chapter 20	Probability

Conclusion

In geometric progression class 10 ICSE, geometric progression is a sequence of numbers in which each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio (r). If you’re enthusiastic about enhancing your expertise and cultivating a more profound comprehension of the concepts addressed, you’ll discover a plethora of geometric progression class 10 ICSE questions on oswal.io. These educational resources are crafted to support your quest for a deeper grasp of the subject matter, empowering you on your educational journey.

Frequently Asked Questions

Q1. What is a Geometric Progression (GP)?

Ans: A GP is a sequence of numbers in which each term is obtained by multiplying the preceding term by a constant non-zero number called the common ratio.

Q2. How is the common ratio (r) of a GP calculated?

Ans: The common ratio (r) is calculated by dividing any term in the GP by its preceding term:

\\ r = \frac{a_n}{a_n – 1}

Q3. What is the formula for the nth term of a GP?

Ans: The nth term of a GP is given by:

\\ a_n = a.r^{\left(n – 1\right)}

Q4. How do you find the sum of the first 'n' terms of a GP?

Ans: The sum of the first ‘n’ terms of a GP is calculated using the formula:

\\ S_n = \frac{a(r^n – 1)}{r – 1}.

Q5. What happens if the common ratio (r) is greater than 1 in a GP?

Ans: If r is greater than 1, the GP is increasing, and the terms become larger as the sequence progresses.

Chapter Wise Important Questions for ICSE Board Class 10 Mathematics
Goods and Service Tax (GST)
Banking
Shares and Dividends
Linear inequations
Quadratic Equations in one variable
Ratio and proportion
Factorization
Matrices
Arithmetic Progression
Geometric Progression
Coordinate Geometry
Reflection
Similarity
Loci
Circles
Constructions
Mensuration
Trigonometry
Statistics
Probability

Class 10 Maths Chapter 10 Geometric Progression Important Questions

Introduction

What is Geometric Progression?

Class 10 Geometric Progression Important Questions and Answers

Q1. The 11th term of the G.P.

\frac{1}{8},\frac{-1}{4} ,2,-1,....is

Options

(a) 18(b) 19(c) 20(d) 21

Q2. The list of number.

\frac{1}{9},\frac{1}{3},1,-3…. Is a

Options

(a) G.P. with r = – 3(b) G.P. with r = – 1/3(c) G.P. with r = 3(d) not a G.P.

Q3. The sum of first three terms of a G.P. is 16 and the sum of next three terms is 128. Determine the sum of n terms of the G.P.

Q4. Determine the G.P.

whose 3rd term is 8 and 7th term is \frac{128}{625}

Q5. Express the recurring decimal 0.3 as an infinite G.P. and find its value in rational form.

ICSE Class 10 Maths Chapter wise Important Questions

Conclusion

Frequently Asked Questions

Q1. What is a Geometric Progression (GP)?

Q2. How is the common ratio (r) of a GP calculated?

Q3. What is the formula for the nth term of a GP?

Q4. How do you find the sum of the first 'n' terms of a GP?

Q5. What happens if the common ratio (r) is greater than 1 in a GP?

Contact Us

Class 10 Maths Chapter 10
Geometric Progression
Important Questions

$\frac{1}{8},\frac{-1}{4} ,2,-1,....is$

(a) 18
(b) 19
(c) 20
(d) 21

$\frac{1}{9},\frac{1}{3},1,-3…. Is a$

(a) G.P. with r = – 3
(b) G.P. with r = – 1/3
(c) G.P. with r = 3
(d) not a G.P.

whose 3rd term is 8 and 7th term is $\frac{128}{625}$