Circles

Home / Board / ICSE / important Questions / Class 10 / Maths / Circles

Class 10 Maths Chapter 15
Circles
'Important Questions

Chapter 15 of ICSE Class 10 Mathematics, titled “Circles,” is a fundamental chapter that delves into the geometry of circles. Circles are one of the most important geometric shapes and have numerous applications in mathematics and real-life situations. This chapter introduces students to the properties, theorems, and concepts related to circles, enabling them to solve problems involving circles with confidence. Questions on circles for class 10 ICSE are designed as a valuable tool to help students build confidence in their mathematical skills, alleviate doubts, and overcome difficulties they might encounter while studying this topic. students can strengthen their grasp of this fundamental mathematical concept, making it easier for them to excel in their class 10 Mathematics exams.

Table of Contents

Introduction

Circles of class 10 ICSE are one of the fundamental geometric shapes that have been studied and admired for their simplicity and symmetry since ancient times. In ICSE Class 10 Mathematics, the chapter on circles introduces students to the various aspects of circles, including their definitions, properties, and theorems. Understanding circles is not only crucial for solving geometric problems but also for comprehending more advanced mathematical concepts.
Key Concepts Covered in the Circles Chapter:
Definitions: The chapter begins with the basic definitions of a circle, its center, radius, and diameter. Students learn to distinguish between various parts of a circle, such as arcs, chords, and secants.
Properties of Circles: Students delve into the fundamental properties of circles, including the fact that all points on the circumference are equidistant from the center. They also learn about central angles, inscribed angles, and the relationship between arc lengths and angles.
Circumference and Area: The chapter covers formulas for calculating the circumference and area of a circle. Students practice using these formulas to find measurements in real-world scenarios.

What are Circles?

Circles of class 10 ICSE, Think of a circle as a perfectly round shape, like a pizza or a bicycle wheel. It’s made up of points on the edge, and all these points are the same distance away from a special point right in the middle, which we call the center.
‍Center and Radius: The center is like the heart of the circle, and the distance from this center to any point on the edge is called the radius. So, if you were to stretch your arm from the center to the edge, that’s your radius!
Diameter – Twice the Fun: Now, if you take a line that goes through the center and touches the circle’s edge on both sides, we call that line the diameter. It’s like the circle’s widest smile. Fun fact: The diameter is always twice as long as the radius. That’s a cool math rule (D = 2r)!
‍Circumference – Circle’s Border: The circumference is like the circle’s border or the path you would travel if you walked all the way around it. You can find the circumference by multiplying the diameter by a special number called π (pi). So, it’s C = 2πr or C = πd.
Chords – Connecting Dots: If you join any two points on the circle’s edge with a straight line, that’s called a chord. It’s like connecting dots on a circle.
Arcs and Sectors – Pizza Slices: Imagine cutting a pizza into slices. Each slice has a curved edge, which we call an arc. The area inside a slice, including the curved part and the lines from the center to the edge, is called a sector.

Class 10 Circles Important Questions and Answers

Q1. O is the centre of the circle and ∠POQ = 130°. Find the ∠OPR.

Options

(a) 45°
(b) 65°
(c) 75°
(d) 55°

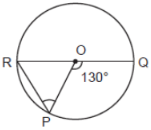
Ans. (b) 65°
Explanation:
since, Angle subtended by an arc at the centre is twice the angle subtended in the remaining part of the circle.
∵ ∠POQ =2∠QRP
$⇒∠QRP = \frac{1}{2} ∠POQ \\ = \frac{1}{2} × 130°×60° \\$ ∵ OP = OR (same radius)
⇒ ∠OPR ×∠ORP= 60°

Q2. The common point of a tangent to a circle and the circle is called:

Options

(a) Point of contact
(b) Secant
(c) Both (a) and (b)
(d) None of these

Ans. (a) Point of contact

Q3. If ABCD is a cyclic quadrilateral in which AD || BC, prove that ∠B=∠C.

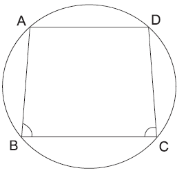
Explanation:
ABCD is a cyclic quadrilateral.
So, ∠ A + ∠ C = 180° …(i)
Since AD || BC
So, ∠ B + ∠ A = 180° …(ii) From equations (i) and (ii),
∠ A + ∠ C = ∠ B + ∠ A
⇒ ∠ C = ∠ B or ∠ B = ∠ C.

Q4. If AB and CD are two chords which when produced meet at P and if AP = CP, show that AB = CD.

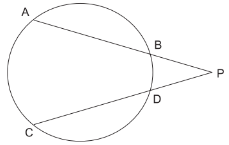
Explanation:
Here, chords AB and CD of the circle intersect at P.
∴ PA × PB = PC × PD
$⇒ PB = \frac{PC×PD}{PA}$

⇒  PB = \frac{AP×PD}{AP}

{˙.˙PC = AP(given)}
⇒ PB = PD…(i)
Now, AB = AP–BP
⇒ AB = CP–PD
[˙.˙AP = CP(given), BP=PD From(i)] But CD = PC–CP
Hence, AB = CD.

Q5. In the figure, AC is the diameter of the circle, centre O. Chord BD is perpendicular to AC. Write down the angles p,q,r in term of x.

Explanation:
In the given circle,
$⇒ ∠ ADB = \frac{1}{2} ∠ AOB = \frac{x}{2} \\ ⇒ ∠ ADB=∠ ACB=q‍ \\ \text{Combining these, we get} \\ \frac{x}{2} = 90° − r = q \\$ ⇒ 2r = 180°–x
and x=2q
∠ DAC=∠ CAB
=∠ BDC
$⇒ p = r =\frac{1}{2}(180° −x)$

Want to Master this Chapter?

Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Download Now

Want to Practice Mock Tests of this chapter

Practice Now

Download Important Questions of this chapter

Download Now

Want to Master this Chapter?

Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Want to Practice Mock Tests of this chapter

Download Important Questions of this chapter

ICSE Class 10 Maths Chapter wise Important Questions

Chapter No.	Chapter Name
Chapter 1	Goods and Service Tax (GST)
Chapter 2	Banking
Chapter 3	Shares and Dividends
Chapter 4	Linear inequations
Chapter 5	Quadratic Equations in one variable
Chapter 6	Ratio and proportion
Chapter 7	Factorization
Chapter 8	Matrices
Chapter 9	Arithmetic Progression
Chapter 10	Geometric Progression
Chapter 11	Coordinate Geometry
Chapter 12	Reflection
Chapter 13	Similarity
Chapter 14	Loci
Chapter 15	Circles
Chapter 16	Constructions
Chapter 17	Mensuration
Chapter 18	Trigonometry
Chapter 19	Statistics
Chapter 20	Probability

Conclusion

In Circles of class 10 ICSE, the study of circles in Class 10 ICSE mathematics is a fundamental part of geometry. Circles are fascinating shapes with unique properties and theorems that help us understand and solve various geometric problems. If you seek additional practice and a deeper comprehension of the topics covered in the chapter, oswal.io offers an extensive array of questions on circles for class 10 ICSE to facilitate a more profound understanding of the concepts.

Chapter Wise Important Questions for ICSE Board Class 10 Mathematics
Goods and Service Tax (GST)
Banking
Shares and Dividends
Linear inequations
Quadratic Equations in one variable
Ratio and proportion
Factorization
Matrices
Arithmetic Progression
Geometric Progression
Coordinate Geometry
Reflection
Similarity
Loci
Circles
Constructions
Mensuration
Trigonometry
Statistics
Probability

Class 10 Maths Chapter 15
Circles
'Important Questions

Introduction

What are Circles?

Class 10 Circles Important Questions and Answers

Q1. O is the centre of the circle and ∠POQ = 130°. Find the ∠OPR.

Options

(a) 45°
(b) 65°
(c) 75°
(d) 55°

Q2. The common point of a tangent to a circle and the circle is called:

Options

(a) Point of contact
(b) Secant
(c) Both (a) and (b)
(d) None of these

Q3. If ABCD is a cyclic quadrilateral in which AD || BC, prove that ∠B=∠C.

Q4. If AB and CD are two chords which when produced meet at P and if AP = CP, show that AB = CD.

Q5. In the figure, AC is the diameter of the circle, centre O. Chord BD is perpendicular to AC. Write down the angles p,q,r in term of x.

ICSE Class 10 Maths Chapter wise Important Questions

Conclusion

Frequently Asked Questions

Q1. What is a circle?

Q2. What is the radius of a circle?

Q3. How is the diameter related to the radius?

Q4. What is the formula for finding the circumference of a circle?

Q5. What is an arc in a circle?

Class 10 Maths Chapter 15 Circles 'Important Questions

Introduction

What are Circles?

Class 10 Circles Important Questions and Answers

Q1. O is the centre of the circle and ∠POQ = 130°. Find the ∠OPR.

Options

(a) 45°(b) 65°(c) 75°(d) 55°

Q2. The common point of a tangent to a circle and the circle is called:

Options

(a) Point of contact(b) Secant(c) Both (a) and (b)(d) None of these

Q3. If ABCD is a cyclic quadrilateral in which AD || BC, prove that ∠B=∠C.

Q4. If AB and CD are two chords which when produced meet at P and if AP = CP, show that AB = CD.

Q5. In the figure, AC is the diameter of the circle, centre O. Chord BD is perpendicular to AC. Write down the angles p,q,r in term of x.

ICSE Class 10 Maths Chapter wise Important Questions

Conclusion

Frequently Asked Questions

Q1. What is a circle?

Q2. What is the radius of a circle?

Q3. How is the diameter related to the radius?

Q4. What is the formula for finding the circumference of a circle?

Q5. What is an arc in a circle?

Class 10 Maths Chapter 15
Circles
'Important Questions

(a) 45°
(b) 65°
(c) 75°
(d) 55°

(a) Point of contact
(b) Secant
(c) Both (a) and (b)
(d) None of these