logo
Log in
logo
Log in
Start Free Trial
Coordinate Geometry

Home / Board / ICSE / important Questions / Class 10 / Maths /Coordinate Geometry

Class 10 Maths Chapter 9
Coordinate Geometry
Important Questions

exam preparation with oswal.io
Chapter 11 of Class 10 Mathematics, “Coordinate Geometry,” is an exploration of a fundamental branch of mathematics that unites algebra and geometry. This chapter introduces students to the concept of representing points and shapes on a coordinate plane, providing a bridge between abstract algebraic equations and visual geometric shapes. Here’s a concise coordinate geometry class 10 ICSE important questions. “In Chapter 11, ‘Coordinate Geometry,’ of Class 10 Mathematics, students embark on a captivating journey that connects the world of algebra with the realm of geometry. This chapter unveils the power of the coordinate plane, where points are represented by ordered pairs (x, y), and equations become geometric shapes.

Introduction

Coordinate geometry class 10 ICSE is an exciting journey that bridges the gap between algebra and geometry. This chapter introduces students to the fascinating world of plotting points on a coordinate plane and discovering the geometric shapes that emerge from algebraic equations. ‍ Coordinate Geometry allows students to represent points in two-dimensional space using ordered pairs (x, y) and explore how these points can create lines, shapes, and patterns. By understanding concepts like slope, distance, and equations of lines, students gain the ability to analyze and describe geometric figures mathematically.

What is Coordinate Geometry?

Coordinate Geometry, often referred to as Cartesian Geometry, as we study in Coordinate geometry class 10 ICSE is a branch of mathematics that combines algebra and geometry. It focuses on the study of geometric shapes and figures using a coordinate system, which assigns numerical coordinates to points in space. This system allows for the precise representation of points, lines, curves, and shapes on a graph.
Here are the key components of Coordinate Geometry:
Coordinate Plane: The fundamental idea in coordinate geometry is the use of a two-dimensional plane known as the Cartesian plane. It consists of two perpendicular lines called the x-axis and the y-axis, which intersect at a point called the origin. The axes divide the plane into four quadrants.
Ordered Pairs: To locate a point on the plane, a pair of numbers (x, y) is used, where “x” represents the horizontal position along the x-axis, and “y” represents the vertical position along the y-axis.
Points: Any location in the plane can be represented by a unique ordered pair (x, y). The point (0, 0) is the origin, where both x and y are zero.
coordinate geometry class 10 icse important questions

Class 10 Coordinate Geometry Important Questions and Answers

Q1.The centroid of a triangle whose angular points are (4, – 3), (5, 6) and (3, – 3) respectively is:
Options
(a) (0, 5)
(b) (4, 0)
(c) (3, – 3)
(d) None of these

Ans. (b)
Explanation:
The co-ordinates of the centroid of a triangle are:
= \begin{pmatrix}  \frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3} \end{pmatrix} \\ = \begin{pmatrix}  \frac{4+5+3}{3},\frac{-3+5-3}{3} \end{pmatrix} \space i.e.(4,0).

Q2. The reflection of the point A(5, – 3) in the point P(3, – 2) is:
Options
(a) (– 5, 3)
(b) (– 3, 2)
(c) (–1, 1)
(d) (-1, 1)

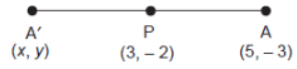
Ans. (b) (– 3, 2)
Explanation:
If A’ (x,y) be the reflection of point A(5, - 3) in the point P(3,-2), then P will be mid - point of AA’.

Coordinate geometry
x= \frac{x_1+x_2}{2} \space and \space y= \frac{y_1+y_2}{2} \\ 3= \frac{x+5}{2} \space and \space - 2 = \frac{y-3}{2} \\ ⇒  x=1 and y =-1
∴ Reflection point will be (1,-1).

Q3. A line passing through the points (a, 2a) and (– 2, 3) is perpendicular to the line 4x + 3y + 5 = 0. Find the value of a.

Explanation:
Let m1 be the slope of the line joining at the points (a, 2a) and (– 2, 3), then,
m_1 = \frac{2a-3}{a+2} \\ \text{Also, slope of the line} \space 4x + 3y + 5 = 0 \\ m_2 = -\frac{4}{3}\\ \text{Since, both the lines are perpendicular.}\\ \text{So,} \space   m_1 m_2 = -1 \\ ∴ \frac{2a-3}{a+2} × \frac{(-4)}{3} = -1 \\ ⇒ 8a – 12 = 3a + 6 \\ ⇒  8a – 3a = 18 \\ ⇒ 5a = 18 \\ ⇒ a = \frac{18}{5} \\ ⇒ a = 3 \frac{3}{5}

Q4. Find the equation of a line that has Y-intercept 3 units and is perpendicular to the line joining (2, – 3) and (4, 2).

Explanation:
Let m be the slope of required lineSlope of the given line
= \frac{2+3}{4-2} = \frac{5}{2} But the required line is perpendicular to the given line.
Hence,m × Slope of the given line = – 1
⇒ m× \frac{5}{2}=-1 \\ ⇒ m  = \frac{-2}{5} \\ ∴ Y-intercept, c = 3
Hence, equation of the required line is given by y = mx + ci.e.,
y = \frac{-2}{5} x+3 \\ ⇒ 5y = – 2x + 15
⇒   2x + 5y – 15 = 0.

Q5. The vertices of a ABC are A (3, 8), B (–1, 2) and C (6, –6). Find:
(a) Slope of BC,
(b) Equation of a line perpendicular of BC and passing through A.

Explanation:
Given,
A (3, 8), B (– 1, 2) and C (6, – 6).
(a) Slope of BC(m_1)= \frac{y_2-y_1}{x_2-x_1} = \frac{-6-2}{6-(-1)} = \frac{-8}{7} \\ (b) Slope of a line perpendicular to BC (m) = \frac{1}{m_1} \\ =-\frac{1}{-8/7} = \frac{7}{8} \\ Let, the equation of the line perpendicular to BC and through A be
y – y_1 = m (x – x_1) \\ ⇒ y-8 = \frac{7}{8} (x-3) \\ ⇒ 8(y – 8) = 7 (x – 3)
⇒ 8y – 64 = 7x – 21
⇒ 7x – 8y – 21 + 64 = 0
⇒ 7x – 8y + 43 = 0
Which is the required equation.

Want to Master this Chapter?
Our Practice Tests, Mind Maps, and Key Questions will help!

Download Mind Map of this chapter

Download Now

Want to Practice Mock Tests of this chapter

Practice Now

Download Important Questions of this chapter

Download Now
Want to Master this Chapter?
Our Practice Tests, Mind Maps, and Key Questions will help!
Download Mind Map of this chapter
Download Now
Want to Practice Mock Tests of this chapter
Practice Now
Download Important Questions of this chapter
Download Now

ICSE Class 10 Maths Chapter wise Important Questions

Chapter No.Chapter Name
Chapter 1Goods and Service Tax (GST)
Chapter 2Banking
Chapter 3Shares and Dividends
Chapter 4Linear inequations
Chapter 5Quadratic Equations in one variable
Chapter 6Ratio and proportion
Chapter 7Factorization
Chapter 8Matrices
Chapter 9Arithmetic Progression
Chapter 10Geometric Progression
Chapter 11Coordinate Geometry
Chapter 12Reflection
Chapter 13Similarity
Chapter 14Loci
Chapter 15Circles
Chapter 16Constructions
Chapter 17Mensuration
Chapter 18Trigonometry
Chapter 19Statistics
Chapter 20Probability

Conclusion

In conclusion, the study of Coordinate Geometry in ICSE Class 10 Mathematics offers students a powerful bridge between algebra and geometry, allowing them to precisely represent and analyze geometric shapes and patterns in a two-dimensional plane. By mastering the use of coordinates and equations, students gain essential problem-solving skills that extend far beyond mathematics. Throughout this chapter, students have explored the principles of the Cartesian plane, learned to plot points, find distances between them, calculate slopes of lines, and work with equations that represent geometric figures. These skills are not only valuable for academic success but also for understanding the real-world applications of coordinate geometry in fields such as engineering, physics, and computer science. If you’re eager to sharpen your skills further and develop a deeper grasp of the concepts covered in this chapter, you’ll find coordinate geometry class 10 ICSE important questions available on oswal.io. These resources are designed to assist you in your journey toward a more profound understanding of the subject matter.

Frequently Asked Questions

Ans: Coordinate Geometry is a branch of mathematics that uses a coordinate system to represent points, lines, and shapes on a two-dimensional plane.
Ans: The Cartesian Plane is the grid used in coordinate geometry, consisting of two perpendicular axes, the x-axis and the y-axis, which intersect at the origin (0,0)
Ans: To plot a point, use an ordered pair (x, y), where “x” represents the horizontal position (along the x-axis) and “y” represents the vertical position (along the y-axis).
Ans: The origin is the point where both x and y coordinates are zero, serving as a reference point for all other coordinates on the plane.
Ans: You can use the distance formula: \sqrt{((x_2 – x_1)^2 + (y_2 – y_1)^2)},\space \text{where} \space (x_1, y_1) \space and \space (x_2, y_2)\\ are the coordinates of the two points.
logo
Instagram Linkedin-in Facebook-f Youtube Twitter
logo
Instagram Linkedin-in Facebook-f Youtube Twitter
  • Syllabus
  • Blogs
  • Plans
  • Contact Us
  • Privacy Policy

CBSE Important Questions Class 9

CBSE Important Questions Class 10

CBSE Important Questions Class 12

CBSE Practice Papers

CBSE Practice Papers

ICSE Important Questions Class 9

  • ICSE Class 9 Maths
  • ICSE Class 9 Physics
  • ICSE Class 9 Chemistry
  • ICSE Class 9 Biolog1y
  • ICSE Class 9 History & Civics
  • ICSE Class 9 Geography
  • ICSE Class 9 Computer Applications

ICSE Important Questions Class 10

ICSE Practice Papers

  • ICSE Class 10 Physics
  • ICSE Class 10 Chemistry
  • ICSE Class 10 Biology
  • ICSE Class 10 Maths

ISC Important Questions Class 12

ISC Practice Papers

  • ISC Class 12 Physics
  • ISC Class 12 Chemistry
  • ISC Class 12 Biology
  • ISC Class 12 Maths

Contact Us

Head Office : Ground Floor, 1 / 12 Sahitya Kunj, M.G Road Agra 282002, Uttar Pradesh (India)
Phone No.: +91-562 25277711
Mobile No.: +91-7455077222
Email: support@oswalpublishers.in
Corporate Office : Noida One, B 702, B7, Sector 62,
Noida - 201309, Uttar Pradesh
Phone No.: +91-562 25277711
Mobile No.: +91-75348 77222
Email: support@oswalpublishers.in

© Copyright 2024 oswal.io by OSWAL PUBLISHERS Simplifying Exams