logo
Log in
  Get Rs 200 off on Oswal Premium Plan for your board preperatoin! For Class 9th till 12th. Use Coupon Code BOARD200 at checkout.
logo
Log in
Start Free Trial
Some Applications of Trigonometry

Home / Boards / CBSE / Important Questions / Class 10 / Maths / Some Applications of Trigonometry

Class 10 Math Chapter 9
Applications of Trigonometry
Important Questions

exam preparation with oswal.io
Here are some important questions for Class 10 Mathematics Chapter 9, Applications of Trigonometry, carefully selected to help students prepare for the CBSE Class 10 Mathematics Examination in 2024-25. These questions cover various real-life applications of trigonometry and are designed to assist students in comprehending its practical uses.

Introduction

In Chapter 9 of Class 10 Mathematics, Application of Trigonometry, In this chapter, students are introduced to simple problems on heights and distances involving angles of elevation and depression. The problems are restricted to angles of 30°, 45°, and 60° and typically do not involve more than two right triangles. By solving these problems, students can enhance their understanding of trigonometric applications in real-life scenarios related to heights, distances, and angles.

What is the angle of elevation and angle of depression in trigonometry?

The angle of elevation is the angle formed between the horizontal line and the line of sight when an observer looks upward to see an object. On the other hand, the angle of depression is the angle formed between the horizontal line and the line of sight when an observer looks downward to see an object.
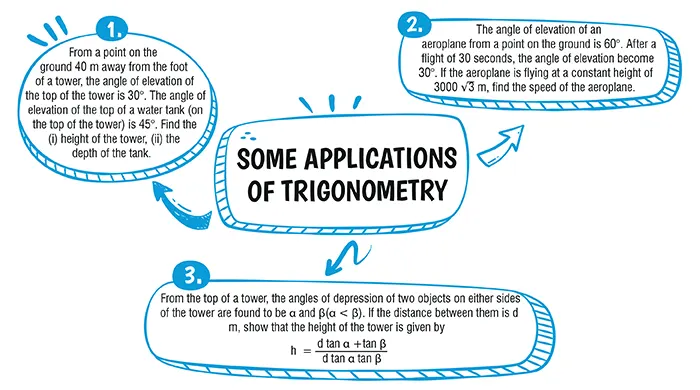
cbse class 10 maths Application of trigonometry important questions and answers

Class 10 Applications of Trigonometry Important Questions and Answers

Q1. A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45°. Then the height (in meters) of the tower is :
Options
(a) 25\sqrt{2}\\ (b) 25\sqrt{3}\\ (c) 25
(d) 12.5

Ans.(c) 25
Explanation:
Let the height of the tower be H m.

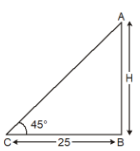
cbse class 10 maths Application of trigonometry important questions and ansers
\text{Thus, tan 45}^o = \dfrac{\text{perpendicular}}{\text{Base}}\\ \text{Or } \dfrac{\text{H}}{25} = 1 \\ \text{Hence, H = 25m}
Q2. The angle of depression of a car standing on the ground from the top of a 75 m high tower is 30°. The distance of the car from the base of the tower (in m) is :
Options
(a) 25 \sqrt{3}\\ (b) 50 \sqrt{3}\\ (c) 75 \sqrt{3}\\ (d) 150

Ans. (c) 75 \sqrt{3}\\Explanation:
Let the distance of the car from the base of the tower be x m.

cbse class 10 maths Application of trigonometry important questions and ansers

Height of tower = 75 m
\\ \text{tan 30}^o = \dfrac{\text{perpendicular}}{\text{base}}\\ ⇒ \dfrac{1}{\sqrt{3}} = \dfrac{75}{x}\\ ⇒ x = 75 \sqrt{3} \\ Thus, distance of the parked car from the
base of the tower is 25 \sqrt{3}

Q3. From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30°. The angle of elevation of the top of a water tank (on the top of the tower) is 45°. Find the (i) height of the tower, (ii) the depth of the tank.

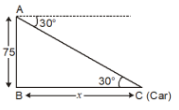
Ans.The height of the tower is h = 23.1 m and the depth of the tank is h= 16.9 m
Explanation:
Let BC be the tower of height h m and CD be the water tank of height h_1 m. Let A be a point on the ground at a distance of 40 m away from the foot B of the tower.

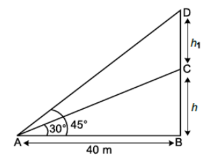
Applications of Trigonometry Q3
\text{In ∆ABD,tan 45°} = \dfrac{BD}{AB}\\[4.5 bp] ⇒ 1 = \dfrac{h + h_1}{40}\\ ⇒ h + h_1 \text{= 40 m ...(i)} \\[4.5 bp] In ∆ABC, we have
\text{tan 30}^o = \dfrac{BC}{AB}\\[4.5 bp] ⇒ \dfrac{1}{\sqrt{3}} = \dfrac{h}{40}\\[4.5 bp] ⇒ h = \dfrac{40}{\sqrt{3}}m \\[4.5 bp] = \dfrac{40\sqrt{3}}{3}m \\[4.5 bp] \\[4.5 bp] = 23.1 m
On putting the value of h in equation (i), we have
\\23.1 + h_1 = 40 \\[4.5 bp] ⇒ h_1 = (40 - 23.1)m \\[4.5 bp] ⇒ = 16.9 m \\[3.5 bp] Thus, the height of the tower is h = 23.1 m and the depth of the tank is h = 16.9 m.

Q4. The angle of elevation of an airplane from a point on the ground is 60°.After a flight of 30 seconds, the angle of elevation becomes 30°. If the airplane is flying at a constant height of 3000
\sqrt{3}\text{m find the speed of the airplane.}

Ans. The speed of the airplane is 720 km/hr.
Explanation:
Let the ground distance between the airplane A and the point E be x m.

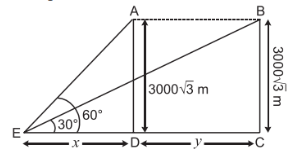
cbse class 10 maths Application of trigonometry important questions and ansers

Given, height AD is 3000 \sqrt{3} \text{m } and the angle of elevation is 60°
So, in ∆AED,
\text{tan 60}^o = \dfrac{3000\sqrt{3}}{x} \\ ⇒ \sqrt{3} = \dfrac{3000\sqrt{3}}{x}\\ \text{⇒ x = 3000 m }\\ Let the new distance (DC) covered by the airplane in 30 seconds be y m.
\\ \text{So, tan 30}^o = \dfrac{3000\sqrt{3}}{3000 + y} \\[4.5 bp] ⇒ \dfrac{1}{\sqrt{3}}= \dfrac{3000\sqrt{3}}{3000 + y}\\[4.5 bp] ⇒ 3000 + y = (3000\sqrt{3})\sqrt{3}\\[4.5 bp] ⇒ 3000 + y = 9000\\[4.5 bp] \text{⇒ y = 9000 - 3000 = 6000 m}\\[4.5 bp] Thus, distance covered in 30 seconds = 6000 m
\\ \text{Hence, Speed = } \dfrac{6000}{30} \\ \text{= 200 m/sec}\\ = 200 × \dfrac{18}{5}\text{km/hr.}\\ Hence, the speed of the airplane is 720 km/hr.

Q5. From the top of a tower, the angles of depression of two objects on either side of the tower are found to be α and β(α < β). If the distance between them is d m, show that the height of the tower is given by
\text{h} = \dfrac{\text{d tan α + tan β}}{\text{d tan α tan β}}

Explanation:
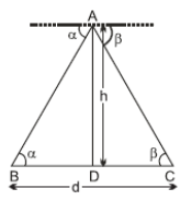
Let AD be the tower and B, C be the two objects on either side of AD.

Given, BC = d = BD + DC and AD = h
\\\text{In ∆ADB, tan α = } \dfrac{AD}{BD} \\

Applications of Trigonometry Q5
\text{⇒ tan α = } \dfrac{h}{BD} \\[4.54 bp]\text{⇒ h = BD tan α …(i)} \\[4.54 bp]\text{In ∆ADC, tan β} = \dfrac{AD}{DC}\\[4.5 bp]\rArr \text{tan β } = \dfrac{h}{\text{DC}} \\[4.5 bp] ⇒ h = DC tan β …(ii)
Thus, from equations (i) and (ii), we get
BD tan α = DC tan β
⇒ (D - DC) tan α =DC tan β
⇒ d tan α = DC( tan α + tan β)
\\[4.5 bp]⇒ \text{DC} = \dfrac{\text{d tan α}}{\text{tan α + tan β}} \\ [4.5 bp]Substituting the value of DC in (ii), we get
\\[4.54 bp]\text{h = } \dfrac{\text{d tan α}}{\text{tan α + tan β}}\text{tan β} \\[4.54 bp]⇒ \text{h = } \dfrac{\text{d tan α tan β}}{\text{tan α + tan β}}
Download PDF

CBSE Class 10 Maths Chapter wise Important Questions

making of global world class 10 important questions

Conclusion

For a better understanding of the Applications of Trigonometry chapter, visit oswal.io. This platform provides a variety of practice questions tailored for easier learning. By working on these questions, you can reinforce your grasp of how trigonometry is used in real-life situations and improve your problem-solving abilities. It’s a great way to practice and boost your confidence in dealing with practical trigonometric scenarios.

Frequently Asked Questions

Ans: To find the height of a building or a tree, one can use the concept of trigonometry. By measuring the angle of elevation from a specific point on the ground to the top of the building or tree and knowing the distance between the observer and the object, we can use trigonometric ratios to calculate the height of the object.
Ans: Trigonometry can be used to find the distance between two objects by measuring the angles of elevation or depression from two different points and knowing the height of one of the objects. By forming two right triangles with the height and the distance between the points, trigonometric ratios can be used to calculate the distance between the objects.
Ans: Trigonometry is commonly used to solve problems involving heights. By measuring the angle of elevation from a reference point to the top of an object and knowing the distance between the observer and the object, trigonometric ratios can be utilized to calculate the height of the object.
Ans:Trigonometry is extensively applied in navigation for determining positions and distances. In marine navigation, for example, sailors use trigonometry to calculate their ship’s position using celestial objects’ angles, like stars or planets. Similarly, in land navigation, GPS systems use trigonometry to determine the distances between different locations.
Ans: In construction and engineering, trigonometry is used for designing and measuring structures. Engineers use trigonometric ratios to calculate distances, angles, and heights of buildings, bridges, and other architectural elements, ensuring precision and stability in construction.
logo
Instagram Linkedin-in Facebook-f Youtube Twitter
logo
Instagram Linkedin-in Facebook-f Youtube Twitter

CBSE Important Questions Class 10

ICSE Important Questions Class 10

CBSE Important Questions Class 10

ICSE Important Questions Class 10

Contact Us

© Copyright 2025 oswal.io by
Oswal Publishers Simplifying Exams