Quadratic Equations

Home / Boards / CBSE / Important Questions / Class 10 / Maths / Quadratic Equations

Class 10 Maths Chapter 4
Quadratic Equations
Important Questions

Here are some important Class 10 Mathematics questions for Chapter 4, Quadratic Equations, thoughtfully curated to aid students in their preparation for the CBSE Class 10 Mathematics Examination 2024-25. By practicing a diverse range of question types, students can clarify doubts and enhance their problem-solving skills, leading to improved performance in the Quadratic Equations chapter.

Table of Contents

Introduction

In Chapter 4 of Class 10 Mathematics,Quadratic Equations we will explore the standard form of a quadratic equation.we will delve into the methods of solving quadratic equations, both by factorization and by utilizing the quadratic formula. And we will discuss the Situational problems based on quadratic equations related to day to day activities to be incorporated.

What are the Quadratic Equations ?

A quadratic equation is a second-degree polynomial equation of the form

ax^2 + bx + c = 0,

where ‘x’ is the variable, and ‘a’, ‘b’, and ‘c’ are constants with ‘a’ not equal to zero. The highest power of ‘x’ in a quadratic equation is 2, making it a second-degree equation. The standard form of a quadratic equation is represented as:

ax^2 + bx + c = 0

Class 10 Quadratic Equations Important Questions and Answers

Q 1. Find the roots of the quadratic equation $2x^2 + x - 1 = 0:$

Options

$\text{(a) -2 and }{\frac{\textbf{1}}{\textbf{2}}} \\ [4.5 bp] \text{(b) 1 and }{\frac{\textbf{1}}{\textbf{2}}}\\[4.5 bp] \text{(c) -2 and }{\Large\frac{\textbf{1}}{\textbf{2}}}$

(d) 1 and 2

Ans. (a)

Explanation:
Given, $\space\space\space\space 2x^2 + x - 1 = 0 \\ [4.5 bp] ⇒ 2x^2 + 2x - x - 1 = 0 \\ [4.5 bp] ⇒ 2x (x + 1) - 1 (x + 1) = 0 \\[4.5 bp] ⇒ (x + 1)(2x - 1) = 0 \\[4.5 bp] ⇒ \text{x = -1 or x =}{\Large\frac{1}{2}} \\ [4.5 bp] \text{Hence roots of equation are -1 and }{\Large\frac{1}{2}}$

Q 2. For what value of p, the quadratic equation $2x^2 + px + 3 = 0$ has two equal roots?

Options

(a) 8
$\textbf{(b)}2\sqrt{6}\\[4.5 bp]$ (c) 5
$\textbf{(d)} 6\sqrt{6}$

Ans. (c)

Explanation:
For a given equation to have equal roots

D = 0,
$\space\space\space\space\space D = b^2 - 4ac$

i.e.
Here, b = p, a = 2, c = 3
$⇒ p^2 - 4 × 2 × 3 = 0 \\ [4.5 bp] ⇒ p^2 - 24 = 0 \\ [4.5 bp] ⇒ \text{p = } \pm \sqrt{24} = \pm 2\sqrt{6} \\ [4.5 bp] \text{Hence, for} \space p = \pm 2\sqrt{6} \space \text{the given equation has equal roots.}$

Q 3. For what value of k, the quadratic equation $kx^2$ + 11x – 4 = 0 has real roots?

Explanation:
Given quadratic equation is

Kx^2 + 11x - 4 = 0 \\ [4.5 bp] \text{On comparing with} \space ax^2 + bx + c = 0,\text{we get} \\[4.5 bp] a = k, b = 11, c = - 4 \\ [4.5 bp] ∵     \text{It has real roots. } \\[4.5 bp] ∴       D\geq 0 \\[4.5 bp] ⇒        b - 4ac\geq 0 \\[4.5 bp] ⇒     (11) - 4 × k × (- 4)\geq 0 \\[4.5 bp] ⇒     121 +  16k \geq 0 \\[4.5 bp] ⇒    \text{k}\geq {\Large \frac{-121}{16}}

Q 4. A girl is twice as old as her sister. Four years hence the product of their ages (in years) will be 160. Find their present ages.

Explanation:
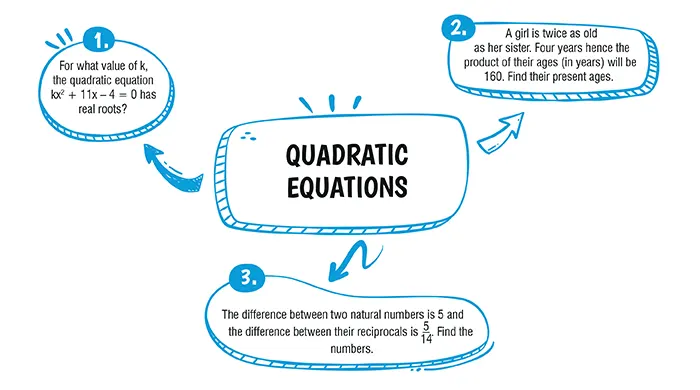
Let the sister’s age be x. Thus, the girl’s age is 2x.
Four years hence,
       Sister’s age = (x + 4)
and     Girl’s age = (2x + 4)
Now     (x + 4) (2x + 4) = 160
$⇒      2x^2 + 8x + 4x + 16 = 160 \\ [4.5 bp] ⇒      2x^2 + 12x + 16 = 160 \\[4.5 bp] ⇒      2x^2 + 12x – 144 = 0 \\[4.5 bp] ⇒      x^2 + 6x – 72 = 0 \\[4.5 bp] ⇒      x^2 + 12x – 6x – 72 = 0 \\[4.5 bp] ⇒      x(x + 12) – 6(x + 12) = 0 \\[4.5 bp] ⇒      (x + 12) (x – 6) = 0 \\[4.5 bp] ⇒      x = 6 \space or \space – 12 \\[4.5 bp] ⇒      x = 6$

(as age is always positive)
Thus, the sister’s age is 6 years and the girl’s age is 2 × 6 = 12 years.

Q 5. The difference between two natural numbers is 5 and the difference between

their reciprocals is $\frac{5}{14}$ . Find the numbers.

Explanation:
Let the natural numbers be x and 5 + x respectively.
According to the question,
$\frac{1}{x} – \frac{1}{x+5} = \frac{5}{14} \\ [4.5 bp]$ ⇒ 14(x+5) – 14x = 5x(x+5)

⇒       $5x^2 + 25x = 70 \\ [4.5 bp]$ ⇒      $x^2 + 5x - 14 = 0 \\ [4.5 bp]$ ⇒       $x^2 + 7x - 2x - 14 = 0 \\ [4.5 bp]$ ⇒     x(x + 7) - 2(x + 7) = 0
⇒     (x + 7) (x - 2) = 0
⇒     (x + 7) (x - 2) = 0
⇒     x = 2, – 7
Since natural numbers cannot be –ve, so x = 2 and x + 5 = 2 + 5 = 7
So, the two numbers are 7 and 2.

CBSE Class 10 Maths Chapter wise Important Questions

Chapter No.	Chapter Name
Chapter 1	Real Numbers
Chapter 2	Polynomials
Chapter 3	Pair of Linear Equations in Two Variable
Chapter 4	Quadratic Equations
Chapter 5	Arithmetic Progressions
Chapter 6	Triangles
Chapter 7	Coordinate Geometry
Chapter 8	Introduction to Trigonometry
Chapter 9	Some Applications of Trigonometry
Chapter 10	Circles
Chapter 11	Areas Related to Circle
Chapter 12	Surface Areas and Volumes
Chapter 13	Statistics
Chapter 14	Probability

Conclusion

If you want to improve your understanding of the concepts in this chapter, you can visit oswal.io. They have a wide range of questions that will help you practice and reinforce what you’ve learned. By solving these questions, you can strengthen your knowledge and become better at solving problems.

Frequently Asked Questions

Q1. How many solutions can a quadratic equation have?

Ans: A quadratic equation can have two solutions, one solution (double root), or no real solutions (complex roots), depending on the value of the discriminant

(b^2 - 4ac).

If the discriminant is greater than zero, the equation has two distinct real roots.
If the discriminant is zero, the equation has one real root (double root).
If the discriminant is negative, the equation has no real solutions (complex roots).

Q5. What is the difference between a quadratic equation and a linear equation?

Ans: A quadratic equation is a second-degree polynomial equation

(ax^2 + bx + c = 0),

while a linear equation is a first-degree polynomial equation (ax + b = 0). The highest power of the variable ‘x’ in a quadratic equation is 2, while in a linear equation, it is 1.

Chapter Wise Important Questions for CBSE Board Class 10 Maths
Real Numbers
Polynomials
Pair of Linear Equations in Two Variables
Quadratic Equations
Arithmetic Progressions
Triangles
Coordinate Geometry
Introduction to Trigonometry
Some Applications of Trigonometry
Circles
Areas Related to Circles
Surface Areas and Volumes
Statistics
Probability

Class 10 Maths Chapter 4
Quadratic Equations
Important Questions

Introduction

What are the Quadratic Equations ?

Class 10 Quadratic Equations Important Questions and Answers

Q 1. Find the roots of the quadratic equation $2x^2 + x - 1 = 0:$

Options

$\text{(a) -2 and }{\frac{\textbf{1}}{\textbf{2}}} \\ [4.5 bp] \text{(b) 1 and }{\frac{\textbf{1}}{\textbf{2}}}\\[4.5 bp] \text{(c) -2 and }{\Large\frac{\textbf{1}}{\textbf{2}}}$

(d) 1 and 2

Q 2. For what value of p, the quadratic equation $2x^2 + px + 3 = 0$ has two equal roots?

Options

(a) 8
$\textbf{(b)}2\sqrt{6}\\[4.5 bp]$ (c) 5
$\textbf{(d)} 6\sqrt{6}$

Q 3. For what value of k, the quadratic equation $kx^2$ + 11x – 4 = 0 has real roots?

Q 4. A girl is twice as old as her sister. Four years hence the product of their ages (in years) will be 160. Find their present ages.

Q 5. The difference between two natural numbers is 5 and the difference between

their reciprocals is $\frac{5}{14}$ . Find the numbers.

CBSE Class 10 Maths Chapter wise Important Questions

Conclusion

Frequently Asked Questions

Q1. How many solutions can a quadratic equation have?

Q2. Can a quadratic equation have complex roots?

Q3. How can I solve a quadratic equation by factorization?

Q4. How do I determine the number of solutions of a quadratic equation without solving it?

Q5. What is the difference between a quadratic equation and a linear equation?

Class 10 Maths Chapter 4 Quadratic Equations Important Questions

Introduction

What are the Quadratic Equations ?

Class 10 Quadratic Equations Important Questions and Answers

Q 1. Find the roots of the quadratic equation 2x^2 + x – 1 = 0:

Options

\text{(a) -2 and }{\frac{\textbf{1}}{\textbf{2}}} \\ [4.5 bp] \text{(b) 1 and }{\frac{\textbf{1}}{\textbf{2}}}\\[4.5 bp] \text{(c) -2 and }{\Large\frac{\textbf{1}}{\textbf{2}}}

(d) 1 and 2

Q 2. For what value of p, the quadratic equation 2x^2 + px + 3 = 0 has two equal roots?

Options

(a) 8 \textbf{(b)}2\sqrt{6}\\[4.5 bp] (c) 5 \textbf{(d)} 6\sqrt{6}

Q 3. For what value of k, the quadratic equation kx^2 + 11x – 4 = 0 has real roots?

Q 4. A girl is twice as old as her sister. Four years hence the product of their ages (in years) will be 160. Find their present ages.

Q 5. The difference between two natural numbers is 5 and the difference between

their reciprocals is \frac{5}{14} . Find the numbers.

CBSE Class 10 Maths Chapter wise Important Questions

Conclusion

Frequently Asked Questions

Q1. How many solutions can a quadratic equation have?

Q2. Can a quadratic equation have complex roots?

Q3. How can I solve a quadratic equation by factorization?

Q4. How do I determine the number of solutions of a quadratic equation without solving it?

Q5. What is the difference between a quadratic equation and a linear equation?

Class 10 Maths Chapter 4
Quadratic Equations
Important Questions

Q 1. Find the roots of the quadratic equation $2x^2 + x - 1 = 0:$

$\text{(a) -2 and }{\frac{\textbf{1}}{\textbf{2}}} \\ [4.5 bp] \text{(b) 1 and }{\frac{\textbf{1}}{\textbf{2}}}\\[4.5 bp] \text{(c) -2 and }{\Large\frac{\textbf{1}}{\textbf{2}}}$

Q 2. For what value of p, the quadratic equation $2x^2 + px + 3 = 0$ has two equal roots?

(a) 8
$\textbf{(b)}2\sqrt{6}\\[4.5 bp]$ (c) 5
$\textbf{(d)} 6\sqrt{6}$

Q 3. For what value of k, the quadratic equation $kx^2$ + 11x – 4 = 0 has real roots?

their reciprocals is $\frac{5}{14}$ . Find the numbers.